[뉴스스페이스=이종화 기자] 

 

<편집자주> 유튜브, 인스타 등에서 활동하는 인플루언서들이 '협찬을 받지 않았다', '광고가 아니다'라는 사실을 보이기 위해 "내 돈 주고 내가 샀다"라는 뜻의 '내돈내산'이라는 말이 생겼다. 비슷한 말로 "내가 궁금해서 결국 내가 정리했다"는 의미의 '내궁내정'이라고 이 기획코너를 명명한다. 우리 일상속에서 자주 접하는 소소한 얘기거리, 궁금증, 호기심, 용어 등에 대해 정리해보는 코너를 기획했다.
 

 

연애의 세계에서 ‘얼마나 많은 사람을 만나야 할까’라는 질문은 누구나 한 번쯤 고민해본다. 이 세상 모든 사람을 만나보고 나에게 가장 적합한 사람을 선택하면 좋겠지만, 이건 불가능하다. 즉 가능한 한 최대한 많은 사람을 만나야 한다는 단순한 격언이 아니라, 수학적으로 이 수준까지 만나면 크게 확률적으로 어긋남이 없다는 이론이 있다.

 

바로 ‘최적 멈춤 이론(Optimal Stopping Theory)’과 ‘비서 문제(Secretary Problem)’가 그 답을 제공한다.

 

최적 멈춤 이론은 본래 ‘비서 문제(Secretary Problem)’에서 출발해, 여러 후보 중 한 번에 한 명씩 만나면서 지나간 사람은 다시 선택할 수 없는 상황에서 최적의 선택을 하는 방법을 제시한다. 이 원리는 연애뿐 아니라 구직, 집 구하기, 비즈니스 파트너 선정, 심지어 동물의 짝짓기 행동 등에도 적용된다.

 

최적멈춤이론과 37%의 법칙

 

'최적 멈춤 이론'은 여러 선택지 중에서 언제 멈추고 결정해야 가장 좋은 결과를 얻을 수 있는지에 대한 수학적 해법이다. 이를 연애에 적용하면, 인생에서 만날 수 있는 모든 연애 상대의 수를 N이라고 할 때, 처음 M명은 ‘탐색(explore)’ 단계로 삼고, 그 이후에는 이전까지 만난 사람들보다 더 좋은 사람이 나타나면 바로 선택하는 전략이다. 이때 M은 N의 약 37%가 된다.

 

즉, 100명을 만날 수 있다고 가정하면, 첫 37명은 아무리 마음에 들어도 결혼을 미루고, 38번째부터는 이전에 만난 37명보다 더 좋은 사람이 나타나면 바로 선택하는 것이 가장 높은 확률로 최고의 상대를 고를 수 있는 전략이다.

 

심리학과 경제학에서는 이를 ‘탐색(explore)과 확정(exploit)’의 트레이드오프로 설명한다. 즉, 새로운 관계를 맺을지(탐색), 아니면 기존의 관계를 강화할지(확정)의 선택은 인간관계 전반에 걸쳐 중요한 의사결정 문제다.

 

 

그렇다면, 왜 37%인가?…기준선 설정과 확률 극대화

 

연애에서 ‘37% 법칙’이 효과적인 이유는 확률론과 최적 멈춤 이론에 근거한다. 이 전략은 인생에서 만날 수 있는 연애 상대가 한정되어 있고, 한 번 지나친 상대는 다시 선택할 수 없다는 전제에서 출발한다. 실제로 이 법칙은 데이트뿐 아니라 구직, 부동산 거래 등 다양한 불확실한 선택 상황에서 최적의 결정을 내릴 수 있는 수학적 방법론으로 인정받고 있다.

37%는 수학적으로 최적의 기준점이다. 37% 법칙의 핵심은 전체 후보군의 약 37%를 먼저 경험해보고, 그중 최고를 기준선(baseline)으로 삼은 뒤, 이후 만나는 사람 중 기준선보다 더 나은 첫 번째 상대를 선택하는 것이다. 이렇게 하면 최적의 상대를 선택할 확률이 약 37%로, 아무런 전략 없이 무작위로 고르는 것(예: 100명 중 1명, 즉 1%)보다 훨씬 높아진다.

 

이 전략은 ‘너무 빨리 결정하면 더 좋은 사람을 놓칠 수 있고, 너무 늦게 결정하면 이미 좋은 사람을 놓쳤을 수 있다’는 딜레마를 해결한다. 37% 이후에는 최고의 상대를 고를 확률이 가장 높아진다.

 

37% 법칙의 실전 활용기…구직, 구인, 집구하기 등 활용가능성 '무궁무진'

 

실제로 이 공식은 연애뿐 아니라 집 구하기, 직원 채용 등 다양한 상황에 적용된다. 예를 들어 집을 100채 볼 계획이라면, 첫 37채는 정보 수집용으로 삼고, 그 이후에는 이전보다 더 좋은 집이 나오면 바로 계약하는 것이 이론상 최적이다.

 

다만, 선택지의 수를 정확히 알기 어렵거나, 시간적 제약·데이터의 질 등 현실적 한계도 존재한다. 이런 한계는 경험과 직관, 추가적 분석 도구로 보완할 수 있다.

 

직장 내에서 친구나 동료를 선택하거나, 네트워킹을 할 때도 비슷한 논리가 적용될 수 있다. 예를 들어, 새로운 환경에서 다양한 사람들을 먼저 만나보고, 그중에서 자신의 기준에 맞는 사람을 골라 친밀한 관계를 맺는 전략이 있다.

 

다만, 인간관계는 연애처럼 ‘선택 후 돌이킬 수 없는’(no-return) 상황이 아니므로, 완전히 동일하게 적용되지는 않는다. 하지만 ‘탐색(explore)과 확정(exploit)’의 균형을 맞추는 원리는 여전히 유효하다.

 

 

연애 횟수와 수학적 관계…시간으로도 적용가능

연애 횟수가 많을수록 더 좋은 상대를 만날 확률이 높아질까? 단순히 ‘많이 만나는 것’이 아니라, ‘최적의 시점’에 멈추는 것이 핵심이다. 만약 평생 10명의 연애 상대를 만날 수 있다고 가정하면, 첫 4명(37%에 가까운 수)은 ‘탐색’ 단계로 삼고, 5번째부터는 이전보다 더 좋은 사람이 나타나면 바로 선택하는 것이 확률적으로 가장 유리하다.

 

연애 상대의 수를 정확히 알기는 어렵기 때문에, ‘연애 기간’으로 적용하는 방법도 있다. 예를 들어 18세부터 40세까지 연애를 한다면, 22년 중 37%인 약 8년이 지난 26세 이후에 만나는 사람 중 이전보다 더 좋은 사람을 선택하는 전략이다.

 

실생활 적용과 한계

이론은 간단하지만, 실제 연애에서는 다양한 변수가 존재한다. 상대방도 선택의 주체이고, 사람의 성격과 상황은 수학적 모델로 완전히 설명할 수 없다. 또한, ‘최고의 상대’를 찾는 것이 아니라 ‘충분히 좋은 상대’를 찾는 것을 목표로 가져간다면, 전략을 조금 더 유연하게 적용할 수도 있다.

 

어차피 연애에서 많은 사람을 만나야 하는 이유는, 다양한 상대를 경험하며 자신의 기준을 설정하고, 최적의 시점에 멈춰서 최고의 상대를 고를 확률을 높이기 위함이다. 수학적으로는 ‘37% 룰’이 이를 뒷받침하며, 이는 연애뿐 아니라 인생의 다양한 선택에서도 적용될 수 있는 보편적 전략이다.

 

‘최적 멈춤 이론(Optimal Stopping Theory)’과 ‘비서 문제(Secretary Problem)’ 누가 연구?

 

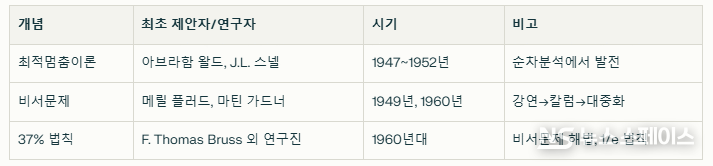
최적멈춤이론(Optimal Stopping Theory)은 확률론과 통계학에서 “언제 멈추는 것이 최적인가”를 연구하는 분야로, 1940년대 후반 아브라함 왈드(Abraham Wald)가 군사 및 산업적 의사결정 지원을 위해 개발한 순차분석(Sequential Analysis)에서 그 기원을 찾을 수 있다. 1952년에는 J.L. 스넬(J.L. Snell)이 일반적 수학적 해법을 제시하며 이론을 체계화했다.

 

비서문제(Secretary Problem)는 1949년 메릴 플러드(Merrill M. Flood)가 “약혼자 문제(fiancée problem)”라는 이름으로 강연에서 처음 제안했다. 1950년대 여러 학회에서 구전되었으나, 공식 논문은 없었다. 이후 1960년 마틴 가드너(Martin Gardner)가 미국 ‘사이언티픽 아메리칸’(Scientific American) 잡지의 ‘수학 게임(Mathematical Games)’ 칼럼을 통해 대중적으로 소개하며 널리 알려졌다.

 

37%의 법칙(The 37% Rule)은 비서문제의 해법 중 하나로, 이 수학적 결론은 1960년대 비서문제 연구 과정에서 도출된 것으로, F. Thomas Bruss 등이 1/e 법칙(37% 법칙)을 수학적으로 정립했다. 이 법칙 자체를 처음 공식화한 단일 인물은 없으나, 비서문제 연구자들과 수학자들이 1960년대 초반에 공동으로 발전시켰다.